|
Reference Links
Topics
Programming Prior Class Pages
PM Wiki |
Main /
HomePageIn the interest of time, this page is built within a wiki framework. The sections on the left are teaching pages that have not been updated for several years (2016). The below is in progress as of March 1, 2025. Research between Jason Krugman + CollaboratorsThis page is a record of a developing set of ideas guided by Jason Krugman Studio in collaboration with Matt Mets, Yevgeny Koramblyum, Phil Ayres, Henry Segerman, Sabetta Matsumoto, Chaim Goodman-Strauss, Nitsan Bartov, Owen Zoyt and others. This set of ideas relates to the subdivision and description of 2 and 3 dimensional space. More specifically, how space is built up and described with increasing information (higher resolution). Starting with a single line, a surface can be described with a mesh of polygons, each created with a minimum of 3 edges. Meshes of triangles offer structurally stable and produce uniformly shaped cells, while quadrilateral mesh offers versatility in topography. Of particular interest in this body of work and research, is the electrification of surfaces and 3 dimensional manifolds. We narrow the scope of the work by assuming that the power must pass through a conductor (not through the air). This helps us focus on the routing problem -- how to get from point A to B (or point X) with at least two conductors (+ and - for DC or live and neutral from AC). MethodIn our light sculpture practice, Krugman Studio uses circuit boards to approximate and physically model many of the shapes and topologies described herein. These physical explorations are complemented by digital models, often made with parametric software such as Rhino 3D and its parametric, module-based plug-in, Grasshopper. The underlying problem that has spurred this line of investigation relates to Krugman's artistic practice, more specifically the design and manufacturing of sculptures that optimize the distribution of electricity in 3-dimensional space, primarily for the purpose of aesthetic beauty. Krugman most commonly uses LED lights to visually define the form of his sculptures and installations. After years of hand-soldering individual LEDs into 4-sided wire meshes, Krugman developed a PCB-based system and corresponding patented IP to distribute electricity through circuit-board-based meshes. 
When manufacturing a structure comprised of PCBs, it is ideal to have as few variations as possible. It is better to have 10,000 pieces all with the same design, rather than 10,000 slightly differing lengths. Each unique instance of a PCB design requires several customized tools and instructions, costing time and money. This open ended research seeks to answer the following questions:
Discrete Edge Form FindingA collaboration between Jason Krugman Studio and Yevgeny Koramblyum (Oom Studios) The goal of this project is to find the most simple and intuitive way of describing physical space, more specifically, the development of complex surfaces from flat, ruled surfaces, and then moving into 3-dimensional manifolds that enclose volumes of 3-D space. We begin by describing a surface constructed with a single, repeated line. We repeat and tile the line in rotations of 60 degrees, forming a plane of equilateral triangles. We can also view the surface as a set of tiled hexagons with the same edge length as our line. Notice how equilateral circles also packed within a plane resolve to a hexagonal layout. Their centerpoints describe a tiled hexagonal surface. 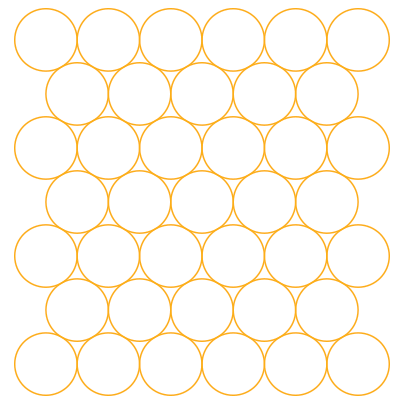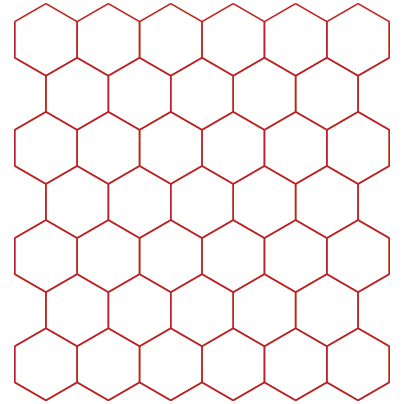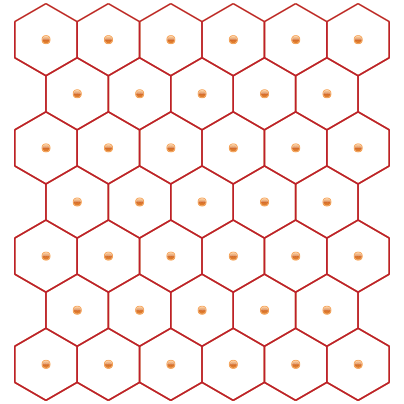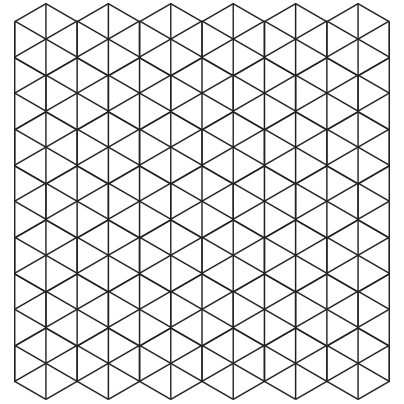 Once we have establish a flat space-filling grid of hexagons broken down into equilateral triangles, we can began to "form" the surface by adding or removing equilateral triangles, or by adding or removing edges from our hexagons. This operation changes the local surface area around the distorted region and creates a bounty or a dearth of "material". This leads to the surface curving inwards or outwards. Removed material causes positive curvature (like a ball) while adding material causes negative curvature (like a saddle). In our examples below, we add or remove a triangle into the existing uniform equilateral triangulated mesh.
In the animation below, we have "doped" a 5 and a 7 sided shape into the orderly 6-valence sheet. This introduces both negative and positive curvature. Without a methodology for re-seaming the sheet, we opened a single channel 1-hexagon wide, and then rejoined the sheet around the 5 and 7 pair. This paper by Phil Ayres et al addresses this methodology more thoroughly. Paper link In the animation below, we show an example of subdivision and use of physical forces to rationalize a surface into uniform hexagons and a single octagonal shape in the center. The eight sided central shape was chosen to correspond with the larger eight sided shape of the entire surface. The surface is "relaxed" using the Kangaroo plugin for Grasshopper (the software used to subdivide this surface). Artwork by Jason Krugman StudioKrugman has designed and created various electrified geodesic structures of sizes ranging from 12" diameter up to 22' x 22' x 16'. These sculptures are primarily symmetrical and are constructed predominantly from PCBs, which act both as physical and electrical support.   3V Sphere - Jupiter Chandelier    Gyroid with 4 Lengths - Jupiter System    12 sided symmetrical "Aura" sculpture with 1 length - Jupiter System,     Icosahedra made with the Trelli System'' Jason Krugman Studio - Quantum Face artwork   3 edge length variants for PCBs, 200+ unique snowflakes with laser-cut polystyrene 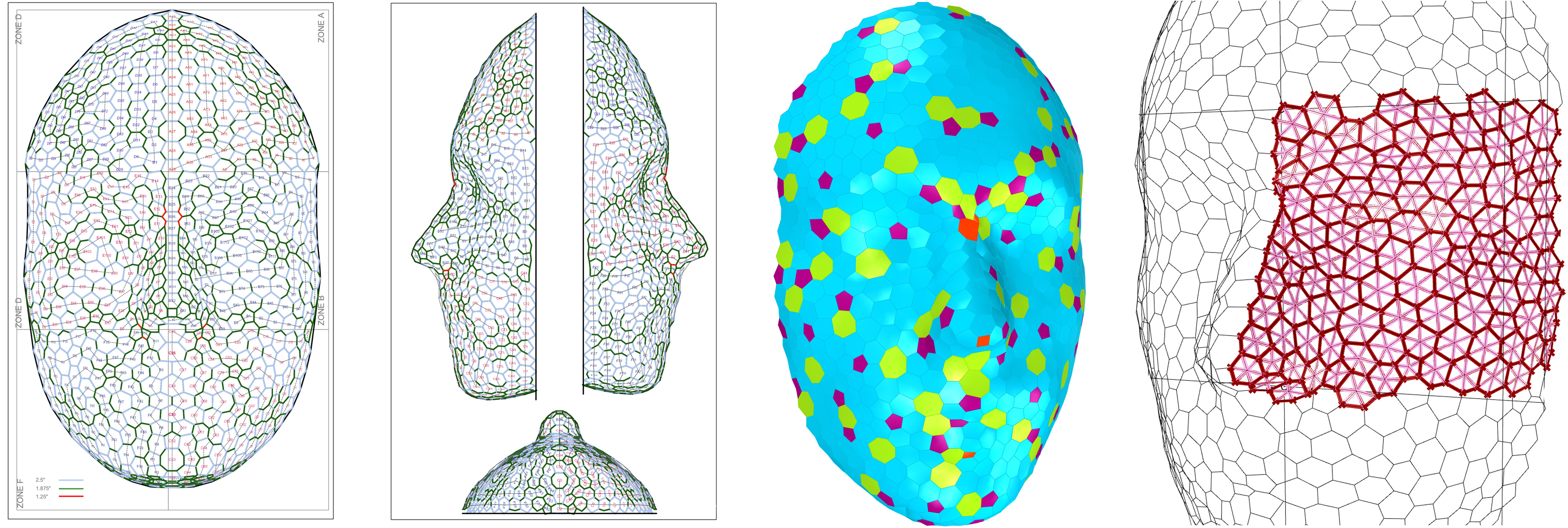 3-D rationalization and software development workflow by Yevgeny Koramblyum, LED sculpture by Jason Krugman Studio Annotated BibliographyIcosahedral Structures
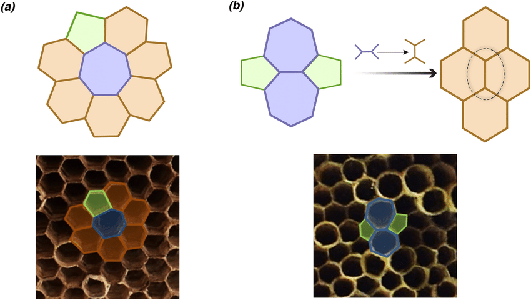 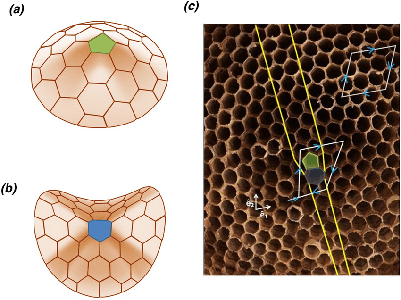
Mathematical Virology - InspirationThe protein capsid layers of many well-known viruses form a variety of icosahedral structures. These structures are made of many proteins twisted and folded into units that tile together into an enclosing layer.
 Carbon Nanotubes and Allotropes of Carbon - InspirationCarbon likes to form hexagonal lattices in both 2 and 3 dimensions. As material science advances, an increasing number of structures are able to be made in laboratories. Nano-scale carbon structures closely parallel larger geodesic strut-based designs and are useful in the search to optimize a variety of these shapes.
   Auxetics - material patterns that can expand when pulled in the opposite directionBeyond Developable - Paper from EPFL - Download, Listing Video  Expanded face of Max Planck from Beyond Developable paper |